สมัยดึกดำบรรพ์
ไม่น่าเชื่อก็ต้องเชื่อนะครับว่า แต่ก่อนเนี่ยไม่มีเลขศูนย์ ไม่มีใครรู้จักเลขศูนย์เลย คนสมัยก่อนนั้นรู้จักการนับแค่ หนึ่ง สอง และมากมาย ครับ หรือถ้าไม่นับแบบนั้น บางแถบก็นับเป็นหน่วยของห้า (ก็นิ้วมือนี่แหละครับ) หรือหน่วยของสิบ (ก็นิ้วมือสองข้าง) หรือหน่วยของยี่สิบ (นิ้วมือนิ้วเท้า)
แล้วทำไมแต่ก่อนคนไม่รู้จักเลขศูนย์ คำตอบง่ายมากครับ คือเพราะเขาไม่ใช้ครับ คณิตศาสตร์ในสมัยก่อนโบราณกาล ก็ใช้นับสัตว์เลี้ยง เวลานับก็เริ่มจากหนึ่ง
หรือพอมีวิทยการมากขึ้นหน่อย ก็เอาตัวเลขมาสัมพันธ์กับเรขาคณิต เพราะฉะนั้นก็ไม่มีเลขศูนย์อยู่ดี พูดกันง่ายๆ ไม่รู้จักเลขตัวนี้ในสารบบ
เลขศูนย์มายังไง
เลขศูนย์นั้นมาจากอินเดียครับ แล้วเข้าสู่ยุโรปหลังจากที่มองโกลนั้นตีตะลุยโลก ทำให้เลขศูนย์นั้นเริ่มเผยแพร่เข้าไปในยุโรป ซึ่งนั่นก็เป็นช่วงคริตศตวรรษที่14 แต่เลขศูนย์นั้นคนเพิ่งเริ่มนิยมเมื่อไม่ถึงสองร้อยปีที่ผ่านมานี้เองนะครับ
แล้วทำไมคนถึงกลัวเลขศูนย์
ลองคิดดูสิครับ ทำไมคนถึงกลัวเลขศูนย์ ศูนย์หารอะไรก็ไม่ได้ คูณอะไรก็ได้ศูนย์ บวกอะไรก็ได้ตัวเดิม เรียกว่าในบรรดาตัวเลจทั้งหมด เลขศูนย์นี่พิเศษสุดๆ
เรื่องนี้เป็นเพราะว่า คนตะวันตกนั้น อยู่ในโลกวิทยาการของกรีกครับ และในปรัชญาของกรีกนั้นอยู่บนพื้นฐานว่าไม่มีช่องว่างครับ ซึ่งก็เหมือนจะไม่ใช่เรื่องใหญ่อะไรใช่ไหมครับ ก็ถ้ามันมีปัญหามาก ก็ทิ้งไปก็ได้
แต่ที่มีปัญหาก็เพราะว่า
จักรวาลของคนกรีกนั้น เชื่อว่าโลกเป็นจุดศูนย์กลางของจักรวาล จากโลกถัดไปก็เป็นดวงจันทร์ เป็นดาวอื่นๆ ไปเรื่อยๆ (เมื่อหลายพันปีมาแล้วนะครับ)
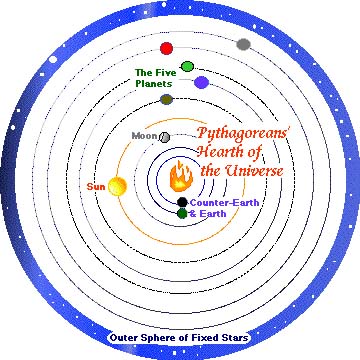
รูปนี้เป็นรูปจักรวาลในความคิดของปิธากอรัส ที่มา http://visav.phys.uvic.ca/~babul/AstroCourses/P303/Images/greek_Pythagorean.jpg
เอาล่ะครับ แล้วก็มีคำถามตามมาครับว่า แล้วใครทำให้โลกหมุน ดาวหมุน ตรงนี้แหละครับที่ทำให้คนตะวันตกนั้นงมโข่งไม่รู้จักเลขศูนย์เป็นพันๆปี
เพราะอริสโตเติลบอกว่า พระเจ้าไง ที่เป็นคนหมุน
ฮั่นแน่ ในเมื่อพระเจ้าเป็นคนหมุน ดังนั้นวิทยาการใหม่ๆที่ท้าทายความคิดเช่นโลกไม่เป็นจุดศูนย์กลาง รวมไปถึงเลขศูนย์ด้วย ก็ย่อมจะไม่เป็นที่พอใจของโบสถ์ และหลายคนได้ถูกฆ่าตายไปก็เพราะว่าไม่เชื่อในพระเจ้านี่แหละ
และเพราะศูนย์นั้นไม่มีในปรัชญากรีก ก็ในเมื่อคณิตศาสตร์ของกรีกนั้น พี่ท่านเอาไปสอดคล้องกับเรขาคณิต เลขศูนย์ก็ไม่รู้จักกันเข้าไปใหญ่ ชาวตะวันตกก็ไม่สนใจเรื่อยมาครับ ทั้งๆที่บางครั้งบางคราวก็มีคนคิดเรื่องนี้ขึ้น
การเริ่มต้นการเดินทางของเลขศูนย์
เลขศูนย์เริ่มเข้ามาพร้อมกับการบุกรุกของชาวมองโกลต่อโลกตะวันตก เมื่อคนมองโกลนั้น เผยแพร่วิทยาการต่างๆมากมายของโลกตะวันออกเข้าสู่โลกตะวันตก (ถ้าอยากรู้เพิ่มเติม เชิญอ่านที่ series ชุดเจงกีสข่านครับ แต่ชุดนั้นไม่มีเรื่องเลขนะครับ)
ในช่วงที่เข้ามาแรกๆนั้น โป๊ปนั้นก็ไม่รู้ว่าเลขศูนย์นี่แหละครับที่จะมาท้าทายถึง ปรัชญาของศาสนาครับ เพราะว่าศูนย์นั้นมาเป็นแพ็คเกจครับ ถ้ามีศูนย์ก็ต้องมีอินฟินีตี้ (infinity หรืออนันต์ไปด้วย)
เพราะฉะนั้นศูนย์ก็เริ่มมีการศึกษาขึ้นครับ แต่เรื่องแรกที่เอาเลขศูนย์มาประยุกต์ใช้คือการวาดรูปครับ แล้วทำไมศูนย์กับอินฟินิตี้นั้นมาคู่กัน ดูรูปนี้เลยครับ

รูปนี้มาจาก http://www.mydigitalnoise.com/images/20051031212952_vanishing%20point%20-%20small.jpg
รูปนี้ก็คือรูป perspective ธรรมดาที่เรารู้จักกันดีใช่ไหมครับ (ภาพที่มีจุดศูนย์กลางของรูป เป็นจุดเดียว) แต่เห็นไหมครับว่าในขณะที่เรามองเห็นไกลสุดกู่ (อินฟินิตี้) เราเห็นสิ่งๆนั้นเป็นจุดครับ
และนี่แหละครับคือจุดเริ่มต้นของการเข้ามาของเลขศูนย์สู่ตะวันตกครับ เมื่อมีศิลปินที่ชื่อ Brunelleschi ได้วาดภาพ perspective รูปแรกของโลกในปี 1425 วิธีการก็คือการมองลอดรูเล็กๆ ผ่านกระจกครับ แล้วรูปแรกก็คือการวาดรูปโดมของเมืองฟลอเรนซ์ครับ (รูปวาดหาไม่เจอครับ แต่เทคนิคและวิธีนั้นดูได้ที่นี่ครับ)
และแล้วเมื่อราวคริตศตวรรษที่ 16-17 เลขศูนย์นั้น ก็เข้ามามีบทบาทมากขึ้น ไม่ว่าจะเป็นการค้นพบความดันบรรยากาศของปาสคาล ที่พบว่ามีสุญญากาศในหลอดบารอมิเตอร์
และแล้วปัญหาเรื่องศูนย์นั้น ก็เริ่มที่จะคลี่คลายลงด้วยดี แต่ช้าก่อน
เลขศูนย์กับแคลคูลัส
เพราะก่อนหน้าที่เราจะรู้จักเลขศูนย์เป็นอย่างดีนั้น มี Calculus เข้ามาครับ ซึ่งคิดโดยทั้งนิวตันและLiebnitz นั้นตอนนั้นก็ยังไม่รู้จักเลขศูนย์เท่าไร แต่ก็คิดแคลคูลัสขึ้นมาได้
แคลคูลัสคืออะไร แคลคูลัสคือวิชาว่าด้วยการหาความเปลี่ยนแปลงครับ เช่น เรารู้ว่าอัตราการเปลี่ยนแปลงของระยะทางต่อเวลา เรียกว่าความเร็ว อัตราการเปลี่ยนแปลงความเร็วต่อเวลา เรียกว่าความเร่ง รวมไปถึงความชันของกราฟก็คืออัตราการเปลี่ยนแปลงเหมือนกัน
แคลคูลัสนั้นก็ว่าด้วยเรื่องพวกนี้แหละครับ
แต่พอเราต้องการหาความเปลี่ยนแปลง ถ้าเราต้องการหาให้ได้แม่นยำที่สุด แล้วทำยังไงครับ
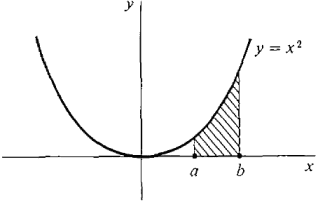
รูปนี้มาจาก http://www.vias.org/calculus/img/04_integration-137.gif
จากรูปด้านบน ถ้าเราต้องการหาความชันของเส้นกราฟ y=x2 ให้ได้แม่นยำที่สุด เราก็ต้องทำให้ a กับ b ใกล้กันมากๆใช่ไหมครับ แล้วใกล้กันที่สุดมันคืออะไรครับ มันก็คือ a=b ถูกไหมครับ แต่ถ้า a=b เราก็จะหาความชันไม่ได้
เพราะว่าความชันคืออัตราส่วน∆y/∆x แต่ถ้า ∆x ซึ่งก็คือ b-a แล้วถ้าเราต้องการใกล้ๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆกันมาก ซึ่งก็คือ ∆x =0
เอาแล้วไงครับ ปัญหามาแล้ว ∆x =0 มันหารไม่ได้!!!!!!!!!
แล้วนิวตันทำยังไง นิวตันก็บอกว่า อ๋อ ดูนะ ถ้าให้ y=x2
มาดูวิธีนิวตันนะครับ
y+Δy=(x+Δx)2
โดยที่ Δ นี่แทนค่าว่า เล็กๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆมากนะครับ
y+Δy=(x+Δx)2=x2+2xΔx+Δx2
แต่เรารู้ว่า y=x2 เพราะเราก็แทนค่าสิครับ
เราก็จะได้ว่า
Δy=2xΔx+Δx2
แล้วคราวนี้มาดูวิธีที่นิวตันบอกครับ นิวตันบอกว่า ก็Δx นี่มันน้อยๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆมากแล้ว Δx2 ยิ่ง น้อยๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆๆเข้าไปใหญ่ เพราะฉะนั้นเอาออกเหอะ ทิ้งไว้ก็เกะกะเปล่าๆ มันก็เลยเหลือแค่นี้ครับ
Δy/Δx=2x แล้วก็จบลงด้วยประการฉะนั้น
แต่ Calculus นั้นมาสมบูรณ์เมื่อ D'Alambert ได้พูดถึง limit ขึ้นมา เราก็ไม่เลยจำเป็นต้องมาคำนึงถึงว่าเราจะเอาศูนย์มาหารอีกต่อไป
นี่แหละครับการเดินทางของเลขศูนย์ในคณิตศาสตร์
แต่ในทางฟิสิกส์นั้น การเดินทางของศูนย์นั้นยังไม่จบครับ เพราะในทางฟิสิกส์นั้น เลขศูนย์คือจุดบรรจบกันของทฤษฏีของนิวตันกับทฤษฏีของไอน์สไตน์ รวมไปถึงจุดกำเนิดทฤษฏีสตริงด้วย และจะเป็นจุดกำเนิดของอีกหลายๆทฤษฏี
โดยสรุปนะครับ
ทฤษฏีนิวตัน ว่าด้วยการเคลื่อนที่ของของชิ้นใหญ่ๆครับ
ทฤษฏีสัมพันธภาพของไอน์สไตน์ ว่าด้วยมีกรอบอ้างอิงที่ไม่ว่าจะวัดอะไรมุมไหน แต่ด้วยกรอบนี้ เป็นกรอบที่สมบูรณ์ ใครอยู่ในกรอบนี้ ก็จะเห็นการเคลื่อนที่เหมือนกัน ไม่ใช่การเคลื่อนที่แบบสัมพัทธ์ (อันนี้มีสี่มิติครับ สามมิติ(กว้าง ยาว สูง) แล้วก็เวลา
ทฤษฏีสตริง ว่าด้วย การอธิบายปรากฏการณ์ต่างๆด้วยการสั่นของเส้น ซึ่งมีถึง 11 มิติ ในการอธิบายปรากฏการณ์ต่างๆ
อันนี้แถมครับ Chaos theory ทฤษฏีมั่วซั่ว เชื่อว่าทุกอย่างถึงแม้มันจะดูว่ามั่วขนาดไหน สิ่งต่างๆเหล่านี้นั้นมีรูปแบบ pattern ซ่อนอยู่เสมอครับ
ที่มา Seife, C. Zero: The bilography of a dangerous idea. Penguin Books, NY. 2000
ขอบคุณข้อมูลจาก http://gotoknow.org/blog/mathbeauty/91599